qraymo Garden

NEA

def NEA akzeptiert ein Wort

$\iff$ es gibt ein Pfad der nach endlich vielen Schritten zu einem akzeptierendem Zustand führt

NEA $\rightsquigarrow$ DEA - durch Potenzmengenkonstruktion

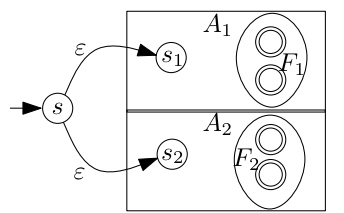
questions Was können NEAs mit Wahlmöglichkeiten, aber ohne $\epsilon$ -Übergänge?

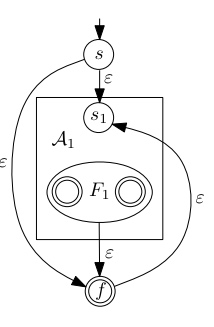
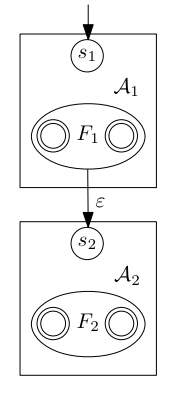
Satz Entfernen von $\epsilon$ -Übergänge

Zu jedem NEA $A$ mit $\epsilon$ -Übergänge gibts einen NEA $\tilde{A}$ ohne $\epsilon$ -Übergänge, der dieselbe Sprache akzeptiert* und nicht mehr Zustände hat da nur Übergänge hinzukommen

Proof Konstruktion durch Anwendung von Erweiterung $\bar{\delta}$ :

$\tilde{\delta} (q,a) =$

${q}$ falls $a = \epsilon$

$\bar{\delta} (q,a)$ sonst

Ein Übergang in $\tilde{A}$ entspricht einer Folge von Übergängen in $A$ von denen genau einer kein $\epsilon$ -Übergang ist, und umgekehrt.

Referenced in

EA

Zu jedem NEA gibt’s einen äquivalenten DEA.

NEA

Zu jedem NEA $A$ mit $\epsilon$ -Übergänge gibts einen NEA $\tilde{A}$ ohne $\epsilon$ -Übergänge, der dieselbe Sprache akzeptiert* und nicht mehr Zustände hat da nur Übergänge hinzukommen

regulär

reguläre Sprache $L$ $\iff$ regulärer Ausdruck α mit $L = L(\alpha)$ $\iff$ NEA $A$ , der $L(\alpha)$ erkennt $\iff$ DEA $\tilde{A}$ , der dieselbe Sprache wie $A$ erkennt