qraymo Garden

reguläre Sprache

def/concept (induktiv) Sprache ist regulär $:\Leftrightarrow$ sr f

Verankerung:

$L = {a}$ mit $a \in \Sigma$ oder

zug. DEA:

$L = {\epsilon}$ oder

zug. DEA:

$L = \varnothing$

dabei $\varnothing$ - regulärer Ausdruck, der leere Menge beschreibt $\rightsquigarrow$ $L(\varnothing) = {}$

zug. DEA:

Im Automatenbereich $:\cong$ EA akzeptiert nie (bzw. kein Wort)

{{TODO}} not sure - to check

nicht äquivalent zu

L = {\epsilon}

oder

Induktion: Es gibt reguläre Sprachen $L_{1}, L_{2}$ , sodass

$L = L_1 \cdot L_2$

NEA dazu:

$L = L_1 \cup L_2$

NEA dazu:

$L = L_{1}^{*}$

NEA dazu:

Proof

Sprache ist regulär $:\Rightarrow$ EA konstruieren

Sprache ist nicht regulär $\Leftarrow:$ PL ist nicht erfüllt

Widerlegen der Aussage des Pumping-Lemmas beweist Nicht-Regularität einer Sprache

Referenced in

[[TGI]] Exam

reguläre Sprachen und [[kontextfreie Sprache]]n

reguläre Sprachen

forward:: reguläre Sprache

regulär

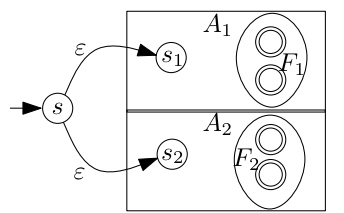
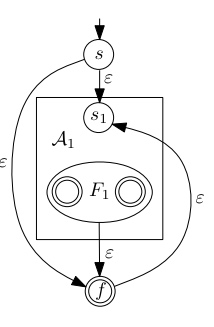
reguläre Sprache $L$ $\iff$ regulärer Ausdruck α mit $L = L(\alpha)$ $\iff$ NEA $A$ , der $L(\alpha)$ erkennt $\iff$ DEA $\tilde{A}$ , der dieselbe Sprache wie $A$ erkennt

PL

def Pumping-Lemma für reguläre Sprache

February 19th, 2021

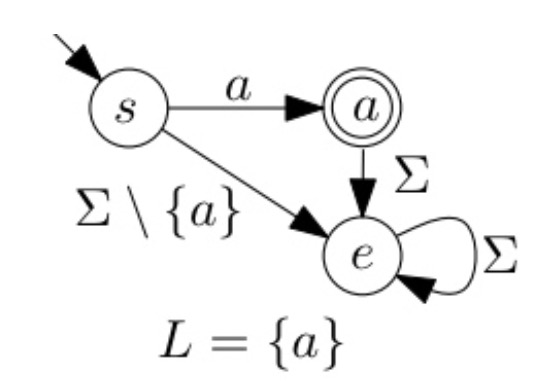
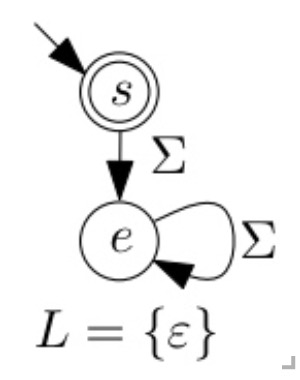
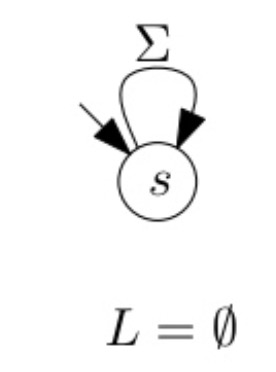
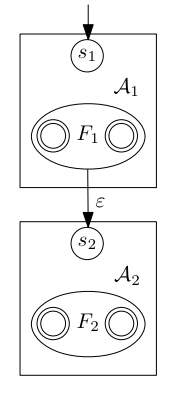
Jede reguläre Sprache $L$ wird von einem (deterministischen) endlichen Automaten akzeptiert. {{7: wbCfktau_}} 📑 sr

Vorlesung-02-Endliche-Automaten.pdf

Satz Jede reguläre Sprache $L$ wird von einem (deterministischen) endlichen Automaten (DEA) akzeptiert. * sr

February 19th, 2021

Jede reguläre Sprache $L$ wird von einem (deterministischen) endlichen Automaten (DEA) akzeptiert. {{7: wbCfktau_}} 📑 sr r/1

Verallgemeintertes [[PL]]

def Verallgemeintertes Pumping-Lemma für reguläre Sprache

EA

reguläre Sprache